Valorile proprii sunt un set special de scalari asociați cu un sistem liniar de ecuații (i.e., o ecuație matricială) care sunt uneori cunoscute și sub numele de rădăcini caracteristice, valori caracteristice (Hoffman și Kunze 1971), valori proprii sau rădăcini latente (Marcus și Minc 1988, p. 144).

Determinarea valorilor proprii și a vectorilor proprii ai unui sistem este extrem de importantă în fizică și inginerie, unde este echivalentă cu diagonalizarea matricelor și apare în aplicații comune precum analiza stabilității, fizica corpurilor în rotație și oscilațiile mici ale sistemelor vibrante, pentru a numi doar câteva. Fiecare valoare proprie este cuplată cu un așa-numit vector propriu corespunzător (sau, în general, un vector propriu drept corespunzător și un vector propriu stâng corespunzător; nu există o distincție analogă între stânga și dreapta pentru valorile proprii).

Descompunerea unei matrice pătrate în valori proprii și vectori proprii este cunoscută în această lucrare sub numele de descompunere proprie, iar faptul că această descompunere este întotdeauna posibilă atâta timp cât matricea formată din vectorii proprii ai este pătrată este cunoscută sub numele de teorema descompunerii proprii.

Algoritmul Lanczos este un algoritm de calcul al valorilor proprii și al vectorilor proprii pentru matrici simetrice mari și rare.

Să fie o transformare liniară reprezentată de o matrice . Dacă există un vector astfel încât

(1)

pentru un anumit scalar , atunci se numește valoarea proprie a lui cu vectorul propriu (drept) corespunzător .

După ce este o matrice pătrată

(2)

cu valoarea proprie , atunci vectorii proprii corespunzători satisfac

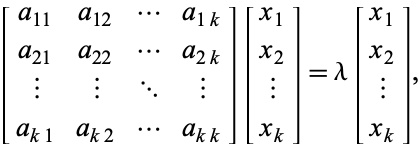(3)

care este echivalent cu sistemul omogen

.

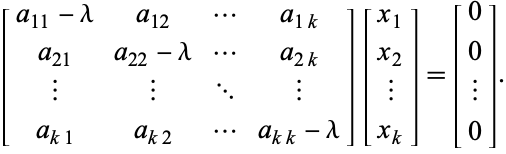(4)

Equația (4) poate fi scrisă compact sub forma

(5)

unde este matricea identitate. După cum se arată în regula lui Cramer, un sistem liniar de ecuații are soluții nontriviale dacă determinantul dispare, astfel încât soluțiile ecuației (5) sunt date de

(6)

Această ecuație este cunoscută sub numele de ecuația caracteristică a lui , iar partea stângă este cunoscută sub numele de polinomul caracteristic.

De exemplu, pentru o matrice , valorile proprii sunt

(7)

care apar ca soluții ale ecuației caracteristice

(8)

Dacă toate valorile proprii sunt diferite, atunci, dacă le introducem din nou, rezultă ecuații independente pentru componentele ale fiecărui vector propriu corespunzător, iar sistemul se spune că este nedegenerat. Dacă valorile proprii sunt de ori degenerate, atunci se spune că sistemul este degenerat, iar vectorii proprii nu sunt liniar independenți. În astfel de cazuri, constrângerea suplimentară ca vectorii proprii să fie ortogonali,

(9)

unde este delta Kronecker, poate fi aplicată pentru a obține constrângeri suplimentare, permițând astfel soluționarea vectorilor proprii.

Valorile proprii pot fi calculate în limbajul Wolfram folosind Eigenvalues. Vectorii proprii și valorile proprii pot fi returnate împreună folosind comanda Eigensystem.

Să presupunem că știm valoarea proprie pentru

(10)

Să adăugăm o constantă ori matricea identitate la ,

(11)

pentru ca noile valori proprii să fie egale cu cele vechi plus . Înmulțind cu o constantă

(12)

pentru ca noile valori proprii să fie cele vechi înmulțite cu .

Considerăm acum o transformare de similitudine a lui . Fie determinantul lui , atunci

.

			(13)
			(14)
			(15)

deci valorile proprii sunt aceleași ca pentru .