Professor Fishers anteckningar om detta ämne i PDF
Professor Fishers bilder om detta ämne i PDF (lösenord krävs)
Gamla bilder från professor Sekula i PDF.

Induktion

Anm. Fisher) skiljer induktion (generalisering av egenskaper hos ett visst urval till andra saker) från abduktion (slutsats till den bästa förklaringen), medan innehållet nedan suddar ut båda dessa tillsammans under den enda rubriken ”induktion”. När du läser den här kursen med professor Fisher är det bättre att förlita dig på hans anteckningar eller diabilder om det här ämnet än på innehållet nedan.

Induktion är en process där man försöker ta reda på hur något fenomen fungerar genom att studera ett urval av det. Man arbetar med ett urval eftersom det inte är möjligt att undersöka varje komponent av fenomenet.Induktion är en kreativ process. Forskaren måste noggrant studera ett exempel på ett fenomen och sedan formulera en hypotes för att förklara fenomenet.Därefter följer den vetenskapliga processen med att testa hypotesen.Forskare som får de mest spektakulära forskningsresultaten är de som är tillräckligt kreativa för att komma på de rätta forskningsfrågorna.

Naturvetenskaperna (fysik, kemi, biologi etc.) är induktiva.Bevis samlas in. Den vetenskapliga metoden tillämpas.Börja med specifika resultat (ett urval) och försök att gissa de allmänna reglerna. Hypoteser kan bara motbevisas, aldrig bevisas. Om en hypotes klarar upprepade försök av många oberoende forskare växer förtroendet för hypotesen. Alla hypoteser är tentativa; vilken som helst skulle kunna vändas i morgon, men det krävs mycket starka bevis för att upphäva en ”lag” eller ett ”faktum”.

Specifik -> Allmän

Här är ett exempel på induktion: Anta att jag har tagit 20 kulor slumpmässigt från en stor påse med kulor. Var och en av dem visade sig vara vit. Det är min observation – varje kula som jag tog ut var vit. Jag skulle därför kunna bilda hypotesen att detta skulle förklaras om alla kulor i påsen var vita. Det kan vara så att det finns några olika färgade kulor i påsen och att mitt första prov helt enkelt inte träffade några.

Detta är för övrigt ett fall där vi skulle kunna bevisa att hypotesen stämmer.Vi skulle helt enkelt kunna slänga ut alla kulor i påsen och undersöka var och en av dem.Ett sådant förfarande kallas för en folkräkning – titta på var och en av dem. I de flesta fall där induktion används är det inte genomförbart.

Abduktion: Detta är en metod för resonemang som inte är rigorös som deduktion.Anta att du har observationer av en intressant händelse. Du är inte omedelbart säker på vad som förklarar observationerna. Du funderar på alla hypoteser du kan som på ett rimligt sätt skulle kunna förklara observationerna.Detta är en kreativ process, till skillnad från deduktion. Du måste veta så mycket som möjligt om situationen för att detta ska fungera bra. Med tanke på allt du vet väljer du den hypotes som verkar mest rimlig och sannolik.Du har valt den uppenbart bästa förklaringen, även om den kan vara felaktig.Det finns ingen garanti. Ytterligare kontroll av din förklaring är vanligtvis en bra idé om det är möjligt; du kan hitta mer information som kan få dig att ompröva din slutsats.

Den här typen av resonemang är Sherlock Holmes starka sida. Conan Doyles berömda hyperobservativa detektiv noterar även mycket små ledtrådar som polisinspektören vanligtvis missar. Holmes kombinerar dessa ledtrådar med den allmänna kunskap han har byggt upp om fallet för att komma fram till den bästa förklaringen – whodunit! Han förklarar också hur brottet utfördes.Som ett trevligt inslag för läsaren förklarar Holmes ofta det resonemang som ledde honom till lösningen. Det verkar enkelt när Holmes förklarar det…

Deduktion

Matematik är en deduktiv vetenskap. Axiom föreslås. De testas inte utan antas vara sanna. Satser härleds från axiomen. Givet axiomen och logikens regler skulle en maskin kunnaproducera satser.

Allmänt -> Specifikt

För att börja med den allmänna regeln och härleda specifika resultat.Om axiomuppsättningen ger upphov till en sats och dessnegation kallas axiomuppsättningen för INCONSISTENT.

För att anta att vi har följande kända förhållanden.

• Vi har en stor påse med kulor.
• Alla kulor i påsen är kända för att vara vita.
• Jag har ett slumpmässigt urval av 20 kulor som tagits från påsen.

Från dessa kan jag dra slutsatsen att alla kulor i urvalet är vita, även utan att titta på dem. Denna typ av resonemang kallas modus ponens (mer om detta nedan och i professor Fishers anteckningar).

Vad sägs om detta?

• Vi har en stor påse med kulor.
• Alla kulor i påsen är vita.
• Jag har ett prov på 20 kulor av blandade färger.

Därav drar jag snabbt slutsatsen att provet inte togs från påsen med vita kulor. Denna typ av resonemang kallas modus tollens (mer om detta nedan och i professor Fishers anteckningar).

Deduktiva argument

Låt oss titta på idén om deduktiva resonemang (hämtad från professor Fishers anteckningar).Här handlar det om att argumentera för någon idé eller slutsats utifrån en uppsättning premisser (fakta, idéer etc.) Prof. Fisher noterar att filosofer brukar visa detta på följande sätt

1. Premise number 12. Premise number 2...------------------------C. Conclusion to be reached

Denna struktur utgör ett argument.Den skrivs ibland som
Premiss 1, Premiss 2, Premiss… => Slutsats.
Låt oss förkorta detta till en syllogism på följande sätt:
P => C (Premiss innebär slutsats, precis som ovan)
Detta betyder helt enkelt att om premisserna är sanna så är slutsatsen också sann.
”För att vara bra måste ett argument ha sanna premisser och premisserna måste ge stöd för slutsatsen. Det starkaste tänkbara stödet skulle ge en absolut garanti för att slutsatsen är sann (under förutsättning, naturligtvis, att premisserna är sanna).Vi kommer att överväga den typen av stöd först, men sedan kommer vi också att överväga några svagare typer av stöd.” (från professor Fisher)

En särskilt användbar typ av argument är ett deduktivt giltigt argument. (Detta förkortas ofta som ”giltigt argument” eller ibland som ”deduktivt argument”.)Deduktivt giltiga argument är argument där premisserna, om de vore sanna, skulle vara det starkaste möjliga beviset för att slutsatsen är sann. Dessa argument ger faktiskt följande garanti: om premisserna är sanna måste slutsatsen också vara sann.
Ett argument som verkar vara deduktivt men som har premisser som inte stöder slutsatsen (ingen garanti) är ett ogiltigt argument.
Låt oss upprepa syllogismen P => C (premisserna leder till slutsatsen).Det finns fyra möjliga påståenden som du kan göra om detta:

1. Alla premisser är sanna (P är sann) (modus ponens-resonemang)
2. En eller flera av premisserna är falska (P är falsk). inte P)
3. Slutsatsen är sann (C är sann)
4. Slutsatsen är falsk (C är falsk – inte C) (modus tollens-resonemang)

Bara två av dessa (nr 1 och 4) utgör deduktivt giltiga resonemang.Låt oss titta på orsaken till detta, ett val i taget.

1. P är sant (P) – Bekräftelse av antecedenten. Om alla premisserna är sanna måste slutsatsen vara sann. Detta är ett mycket starkt argument. (modus ponens)
2. P är falsk (inte P) – Förnekande av antecedenten. Att P är falsk garanterar inte att C är antingen sant eller falskt. Det kan finnas andra orsaker.
3. C är sant (C) – Bekräftar konsekvenserna. Om C är sant kan det bero på en av flera orsaker, inte på denna specifika P.
4. C är falsk (inte C) – Förnekande av konsekvensen. Om C är falsk måste P också vara falsk. Om P var sann skulle C också vara det. (modus tollens)

Kort sagt, #1 och #4 (modus ponens och modus tollens) är deduktivt giltiga medan #2 och #3 inte är det.
Om premisserna gäller för saker i den verkliga världen måste du fortfarande göra ett test för ogiltighet. Det finns minst tre tillvägagångssätt.

1. Se om du kan hitta ett scenario där premisserna är sanna men slutsatsen är falsk.
2. Försök att ersätta ett substantiv eller adjektiv i argumentet med ett annat.Ersätt alla fall. Om detta uppenbarligen inte är giltigt så var originalet inte giltigt.
3. Den som kan göra det är att P är sant men C är falskt.
4. Den som kan göra det är att argumentet är ogiltigt. Vi har gjort dessa diagram åt dig nedan.

Nu tar vi upp ämnet Venndiagram. Dessa kan vara av stort värde när det gäller att kontrollera premisserna i ett argument.

Venndiagram

Venndiagram är en grafisk metod för att representera logik.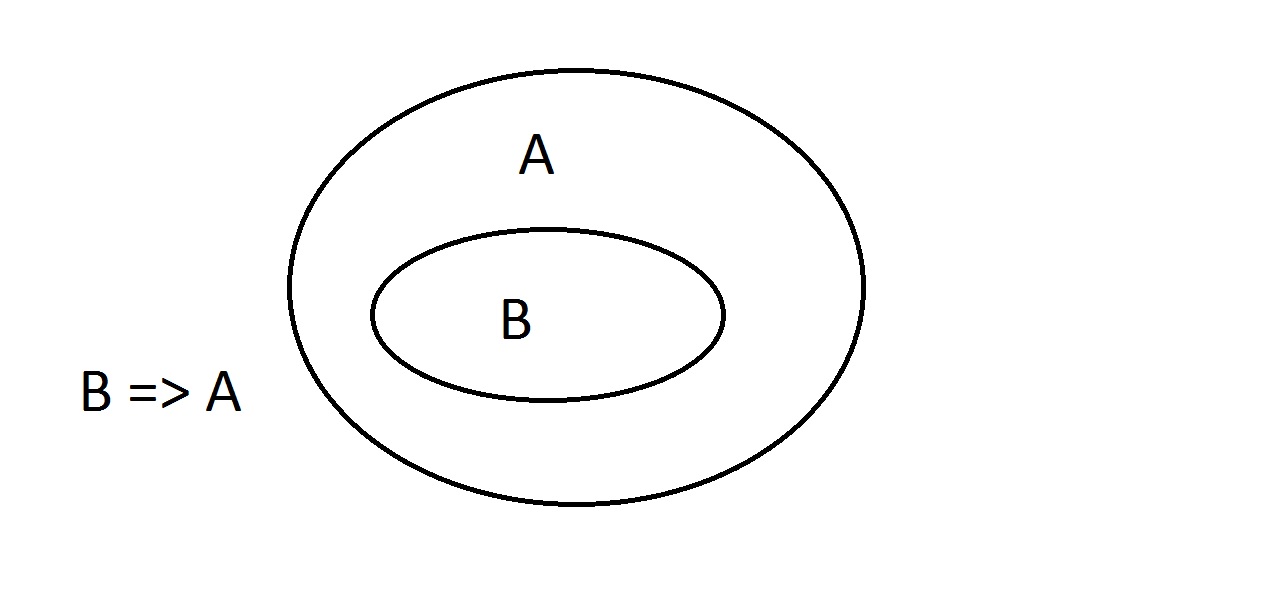
Det här är ungefär det enklaste diagrammet du kommer att få. Den yttre ovalen innehåller alla saker som har egenskapen A, medan den inre ovalen innehåller alla saker som har egenskapen B samt egenskapen A. Detta visas som B=>A, vilket innebär att alla saker som har egenskapen B också har egenskapen A. Man kan också säga att ”B implicerar A”: Om B är sant så måste A också vara det. Detta är den garanti som nämndes ovan.
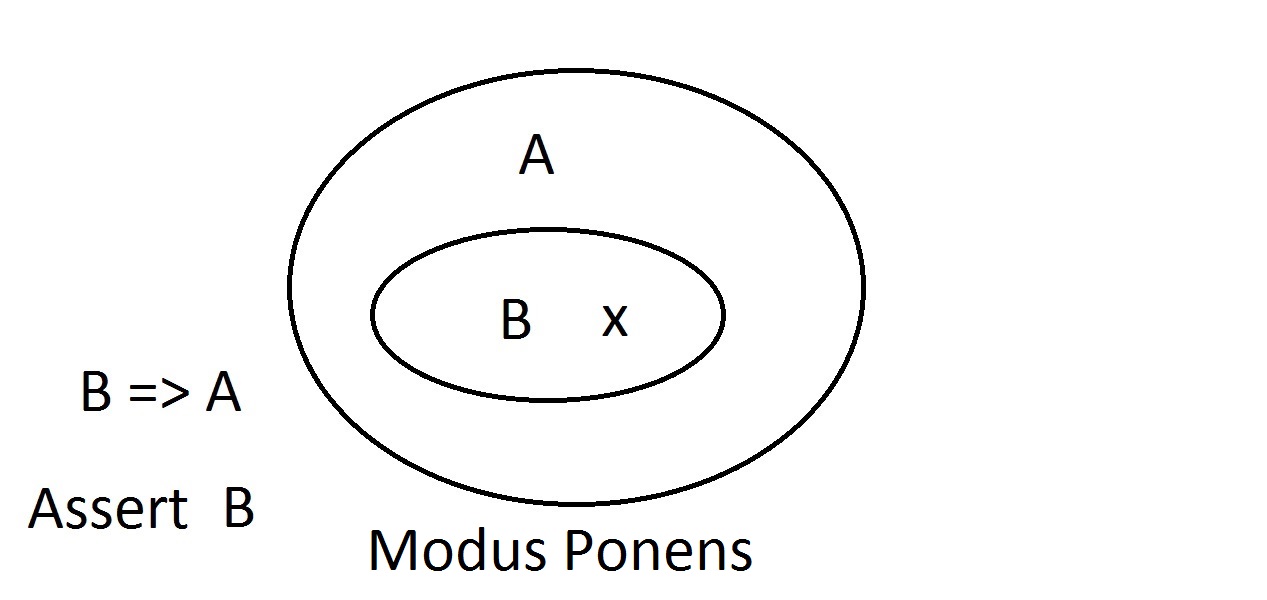Vi kommer nu att hävda att vi har något som har egenskapen B. Vi kan med säkerhet hävda att ithar egenskapen A också. Detta är ett Modus Ponens-resonemang (bekräftelse av antecedenten). Varje enhet med egenskap B måste uppenbarligen också finnas i området med egenskap A.
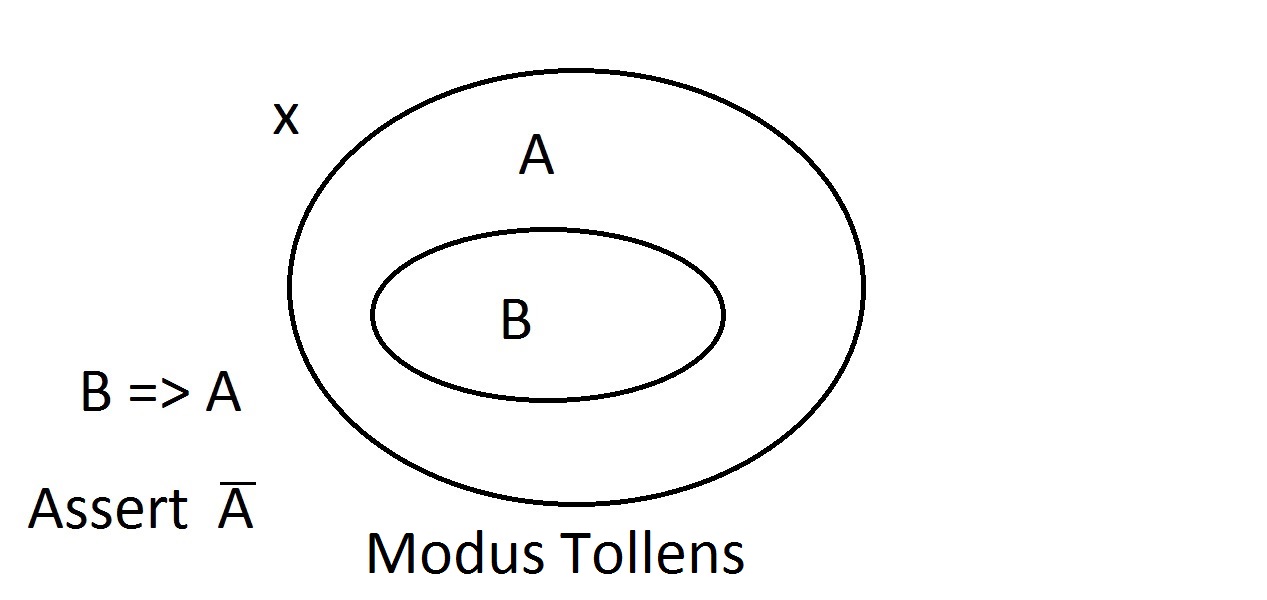Antag att vi nu hävdar att en enhet inte har egenskap A. Venndiagrammet visar att den inte heller kan ha egenskap B. Allt som befinner sig utanför området för egenskap A måste också befinna sig utanför området för egenskap B. Detta är Modus Tollens (förnekande av följden)-resonemang och är giltigt och starkt.
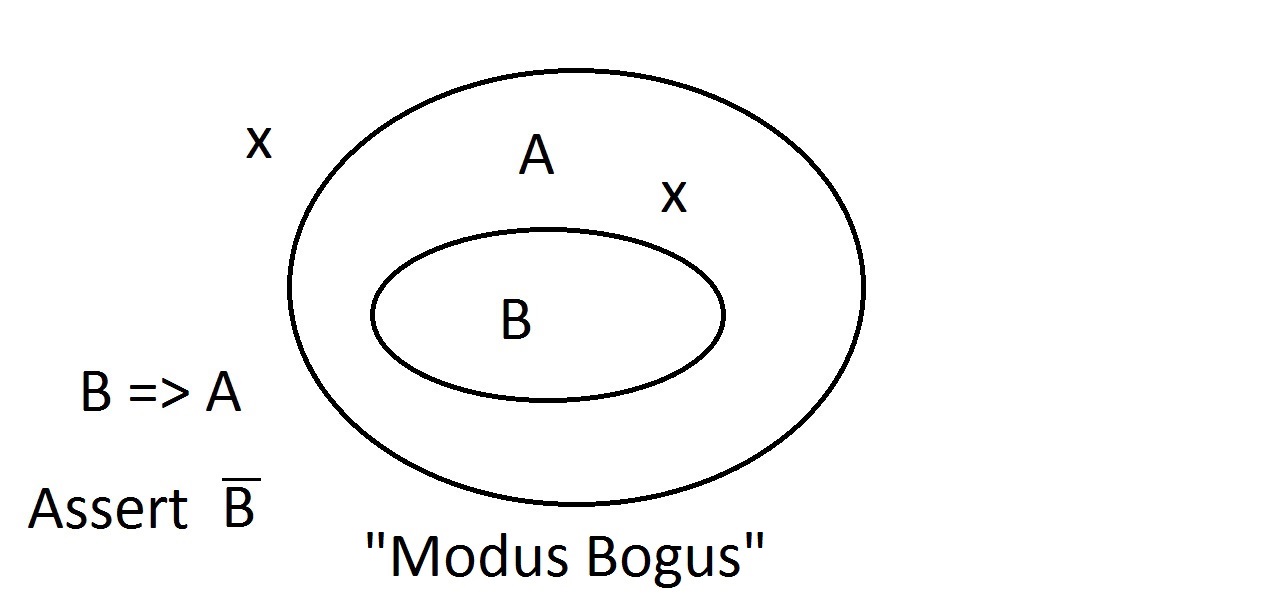Nu ska vi försöka hävda att vårt ting inte har egenskap B. En titt på Venn-diagrammet visar problemet här. En entitet som inte har egenskapen B kan ligga inom A-rummet eller utanför det. Påståendet ”inte B” säger ingenting om A. Detta är inte ett giltigt resonemang, så vi kallade det Modus Bogus. Det är att förneka antecedenten och är inte giltigt.
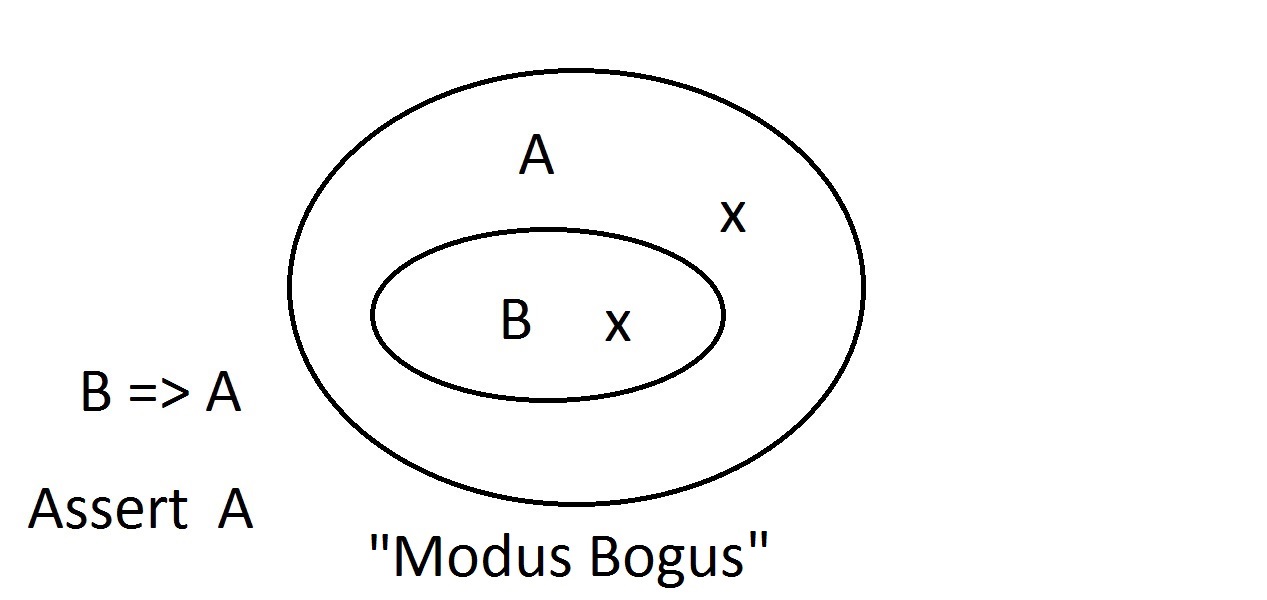Den sista möjligheten är att hävda att vår sak har egenskapen A. Venn-diagrammet visar problemet. Enheten kan ligga var som helst i A-rummet, antingen inom eller utanför B-rummet. Att hävda att saken har egenskapen A säger ingenting om huruvida den också har B. Detta är också Modus Bogus, eller ogiltigt resonemang, och kallas att bekräfta konsekvensen.
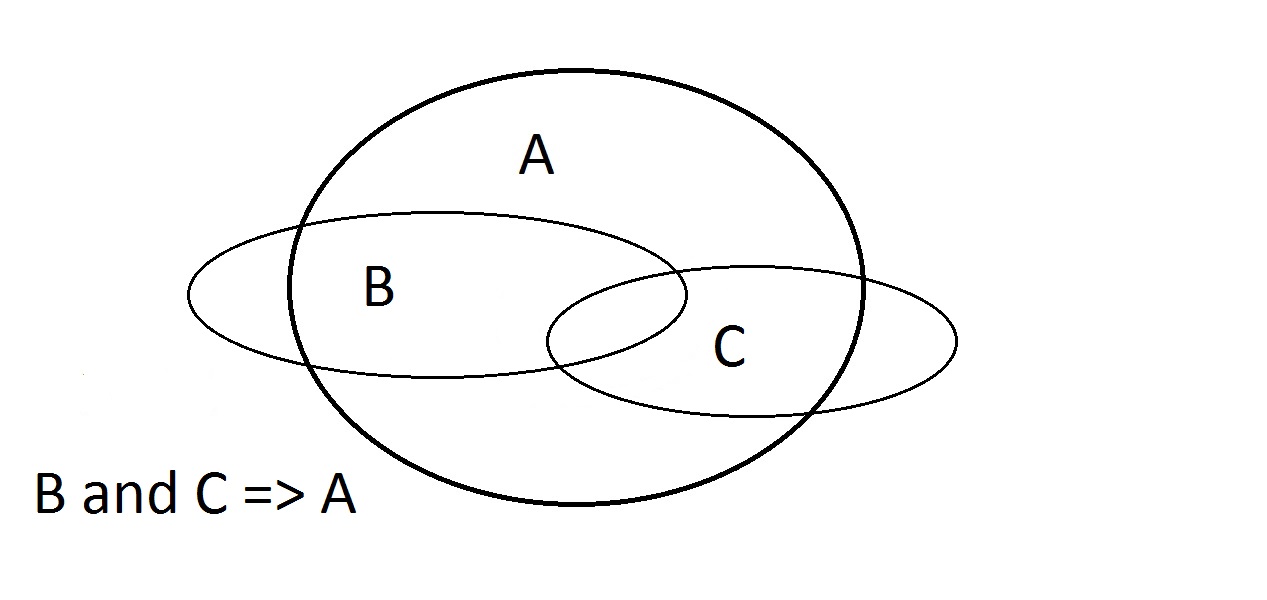Här har vi att göra med egenskaperna A, B och C. Här kan vi bara garantera att en entitet som har B och C också har A. Lägg märke till att en del av B- och C-utrymmena ligger utanför A.

• Assert A: Kan vara var som helst i A
• Assert B: En del av B ligger utanför A
• Assert C: En del av C ligger utanför A
• Assert A och B: Kan inkludera en del av C; kanske inte.
• Assert B och C: Skärningspunkten BC ligger helt och hållet i A. Att argumentera för att B och C => A fungerar.
• Assert A och C: Kan inkludera en del B; kanske inte

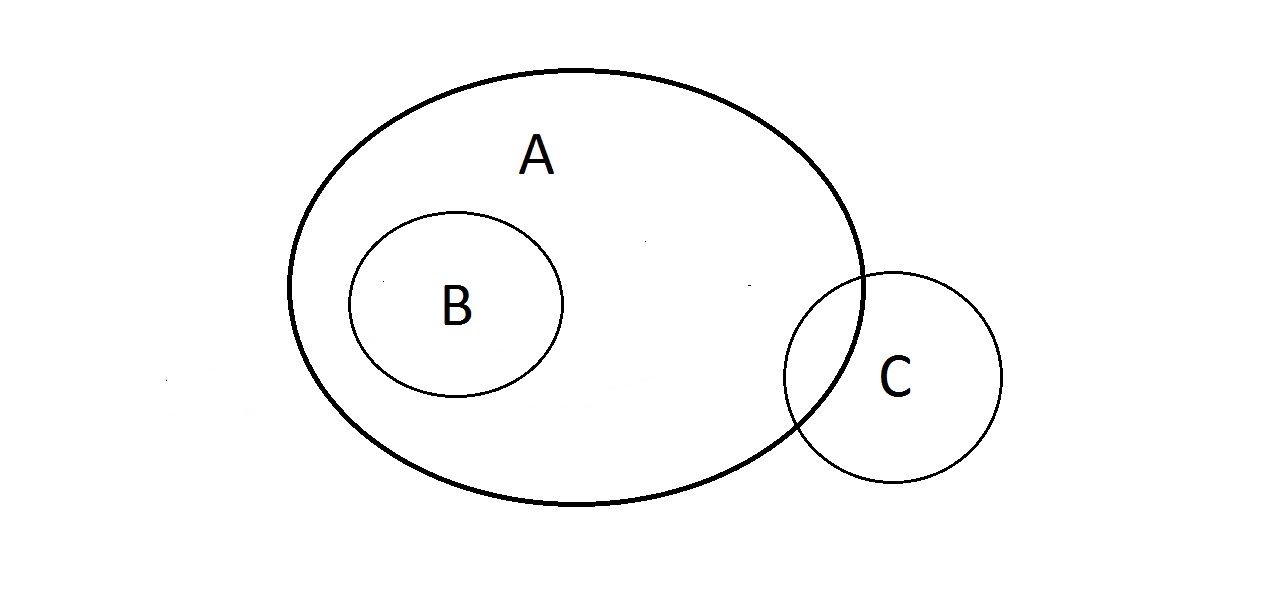
Vad kan man göra med detta? Egenskaperna A och B är som ovan, men hur är det med C? Något som har egenskapen C kan ligga inom A eller inte. Något i A kan också finnas i C eller inte. Du kan inte göra något med C här. Vi har dock en garanti för att något som har B också har A.

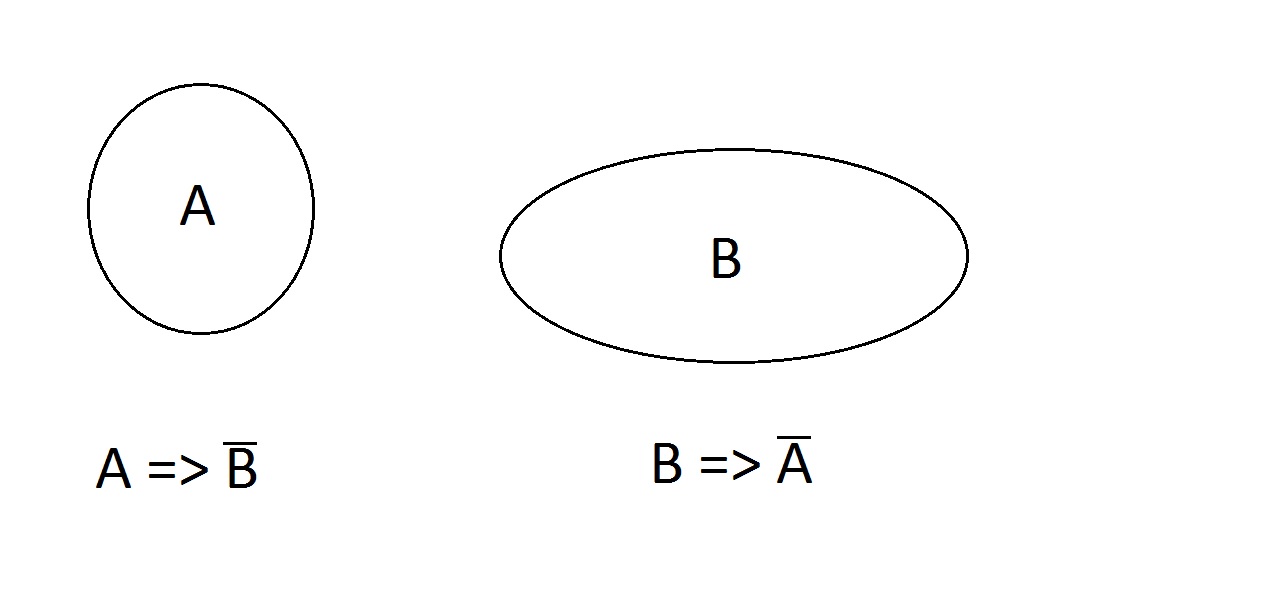
Hur är det med det här? Egenskaperna är exklusiva; en entitet kan inte ha båda samtidigt. den kan ha ingen, A eller B men inte AB. Påståendena A=> inte B och B => inte A är giltiga.
Till sist vill vi att vårt argument ska vara hållbart. För att detta ska ske måste argumentet vara deduktivt giltigt enligt ovan och premisserna måste vara sanna i den verkliga världen. Detta innebär att alla sunda argument är giltiga, men att alla giltiga argument inte nödvändigtvis är sunda.

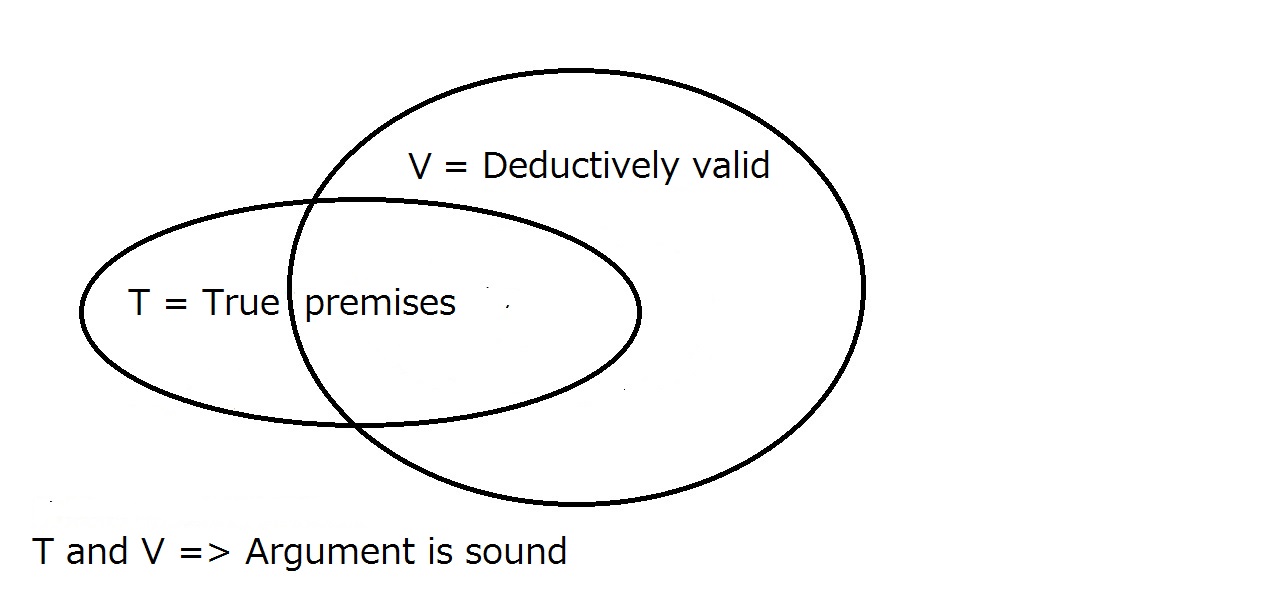
Ett sunt argument kräver att det är deduktivt giltigt och att det har sanna premisser.Att ha det ena garanterar inte automatiskt det andra. Den region som ligger inom bådeT och V är regionen för sunda argument.

Det är så här jag ser det. Alla lyssnar på mig.

Aristoteles (384-322 f.Kr.)

Från http://www.rwe.org/images/aristotle.jpgExperiment?
Självkonsistent?
Om din teori inte är självkonsistent, eller om din teori inte stämmer överens med omsorgsfulla experiment, så är din teori fel. Det spelar ingen roll hur vacker teorin är, den är fel.

Galileo Galilei (1564-1642)

Från http://helios.gsfc.nasa.gov/galileo.jpg

Till exempel Euklids femte postulat.

(1) Genom två olika punkter är det möjligt att dra en linje.
(2) En ändlig rät linje kan förlängas kontinuerligt i en rät linje.
(3) En cirkel kan beskrivas med en valfri punkt som centrum och ett valfritt avstånd som radie.
(4) Alla rätvinkliga vinklar är lika.
(5) Genom en given punkt kan endast en linje dras parallellt med en given linje.
Vorden ”punkt” och ”linje” har ingen inneboende betydelse.
Man skulle kunna byta ut ”punkt” och ”linje” och ändå ha sanna satser.
Man skulle kunna säga
(1) Genom två olika blargar är det möjligt att dra en fleem…
Det femte postulatet kan ändras på två sätt:
(5) Genom en given punkt kan ingen linje dras parallellt med en given linje.
(5) Genom en given punkt kan många linjer dras parallellt med en given linje.
Båda dessa nya postulat ger upphov till olika KONSTANTATIVA geometrier.Vilken av dem är rätt? Alla är det! Vilken av dem beskriver universum?Det är Fysik!