Notele profesorului Fisher pe această temă în PDF
Diapozitivele profesorului Fisher pe această temă în PDF (necesită parolă)
Diapozitivele vechi ale profesorului Sekula în PDF.

Inducție

Nota: Filosofii (inclusiv prof. Fisher) fac distincția între inducție (generalizarea trăsăturilor unui eșantion la alte lucruri) și abducție (inferența la cea mai bună explicație), în timp ce conținutul de mai jos le amestecă pe amândouă sub un singur titlu de „inducție”. Atunci când urmați acest curs cu profesorul Fisher, este mai bine să vă bazați pe notițele sau diapozitivele sale pe această temă, mai degrabă decât pe conținutul de mai jos.

Inducția este un proces prin care se încearcă să se descopere mecanismele unui anumit fenomenprin studierea unui eșantion al acestuia. Se lucrează cu un eșantion deoarece examinarea fiecărei componente a fenomenului nu este fezabilă.Inducția este un proces creativ. Omul de știință trebuie să studieze cu atenție un eșantion al unui fenomen, apoi să formuleze o ipoteză pentru a explica fenomenul.Urmează procesul științific de testare a ipotezei.Oamenii de știință care obțin cele mai spectaculoase rezultate ale cercetării sunt cei care sunt suficient de creativi pentru a se gândi la întrebările de cercetare potrivite.

Științele naturii (fizică, chimie, biologie etc.) sunt inductive.Se colectează dovezi. Se aplică metoda științifică.începeți cu rezultate specifice (un eșantion) și încercați să ghiciți regulile generale. Ipotezele pot fi doar infirmate, niciodată dovedite. Dacă o ipoteză rezistă la încercări repetate de către mai mulți cercetători independenți, atunci crește încrederea în ipoteză. Toate ipotezele sunt provizorii; oricare dintre ele poate fi răsturnată mâine, dar sunt necesare dovezi foarte puternice pentru a răsturna o „Lege” sau un „Fapt”.

Specific -> General

Iată un exemplu de inducție: Să presupunem că am luat 20 de bile la întâmplare dintr-un sac mare de bile. Fiecare dintre ele s-a dovedit a fi albă. Aceasta este observația mea – fiecare bilă pe care am scos-o era albă. Aș putea, prin urmare, să formulez ipoteza că acest lucru s-ar explica dacă toate bilele din pungă ar fi albe. Ar fi necesară o eșantionare suplimentară pentru a testa ipoteza.S-ar putea ca în pungă să existe niște bile varicolore, iar primul meu eșantion pur și simplu nu a nimerit niciuna.

În mod întâmplător, acesta este un caz în care am putea dovedi că ipoteza este adevărată.Am putea pur și simplu să aruncăm toate bilele din pungă și să le examinăm pe fiecare dintre ele.O astfel de procedură se numește recensământ – să ne uităm la fiecare dintre ele. În majoritatea cazurilor în care se folosește inducția, un recensământ nu este fezabil.

Aducție: Inferența la cea mai bună explicație

Aceasta este o metodă de raționament care nu este riguroasă ca Deducția.Să presupunem că aveți observații ale unui eveniment interesant. Nu sunteți imediat sigur de ceea ce explică observațiile. Vă gândiți la toate ipotezele pe care le puteți care ar putea explica în mod plauzibil observațiile.Acesta este un proces creativ, spre deosebire de deducție. Trebuie să știți cât mai multe lucruri posibile despre situație pentru ca acest proces să funcționeze bine. Având în vedere tot ceea ce știți, selectați ipoteza care pare cea mai rezonabilă și probabilă.Ați ales cea mai bună explicație aparentă, deși s-ar putea să fie greșită.Nu există nicio garanție. Verificarea ulterioară a explicației dumneavoastră este de obicei o idee bună, dacă este posibil; ați putea găsi mai multe informații care v-ar putea face să vă reconsiderați concluzia.

Acest tip de raționament este punctul forte al lui Sherlock Holmes. Celebrul detectiv hiper-observator al lui Conan Doyle observă chiar și indicii foarte mici pe care inspectorul de poliție le ratează de obicei. Holmes combină aceste indicii cu cunoștințele generale pe care le-a acumulat despre caz pentru a găsi cea mai bună explicație – whodunit! El explică, de asemenea, cum a fost comisă crima.Într-un mod plăcut pentru cititor, Holmes explică adesea raționamentul care l-a condus la soluție. Pare simplu atunci când Holmes îl explică…

Deducție

Matematica este o știință deductivă. Se propun axiome. Ele nu sunt testate; se presupune că sunt adevărate. Teoremele sunt deduse din axiome. Date fiind axiomele și regulile logicii, o mașină ar puteaproduce teoreme.

General -> Specific

Începeți cu regula generală și deduceți rezultatele specifice.Dacă setul de axiome produce o teoremă și negația acesteia, setul de axiome se numește INCONSISTENT.

Să presupunem că avem următoarele condiții cunoscute.

• Avem o pungă mare de bile.
• Se știe că toate bilele din pungă sunt albe.
• Am un eșantion aleatoriu de 20 de bile luate din pungă.

Din acestea, pot deduce că toate bilele din eșantion sunt albe, chiar și fără să mă uit la ele. Acest tip de raționament se numește modus ponens (mai multe despre acest lucru mai jos și în notele profesorului Fisher).

Ce ziceți de asta?

• Avem un sac mare de bile.
• Toate bilele din sac sunt albe.
• Am un eșantion de 20 de bile de culori amestecate.

Din aceasta deduc rapid că eșantionul nu a fost luat din sacul de bile albe. Acest tip de raționament se numește modus tollens (mai multe despre acest lucru mai jos și în notele profesorului Fisher).

Argumente deductive

Să ne uităm la ideea de raționament deductiv (derivat din notele profesorului Fisher).Aici este vorba despre formularea unui argument pentru o anumită idee sau concluzie pe baza unui set de premise (fapte, idei etc.). profesorul Fisher notează că filozofii arată de obicei acest lucru sub forma

1. Premise number 12. Premise number 2...------------------------C. Conclusion to be reached

Această structură constituie un argument.Uneori se scrie ca
Premisa 1, Premisa 2, Premisa… => Concluzie.
Să prescurtăm acest lucru în silogism astfel:
P => C (Premisele implică concluzia, la fel ca mai sus)
Acest lucru înseamnă pur și simplu că dacă premisele sunt adevărate, atunci și concluzia este adevărată.
„Pentru a fi bun, un argument trebuie să aibă premise adevărate, iar premisele trebuie să ofere suport pentru concluzie. Cel mai puternic sprijin posibil ar oferi o garanție absolută că concluzia va fi adevărată (presupunând, bineînțeles, că premisele sunt adevărate).Vom lua în considerare mai întâi acest tip de sprijin, dar apoi vom trece să luăm în considerare și unele tipuri mai slabe de sprijin.” (de la profesorul Fisher)
Un tip de argument deosebit de util este un argument valid deductiv. (Acesta este adesea prescurtat ca „argument valid” sau, uneori, ca „argument deductiv.”)Argumentele deductiv valide sunt argumente în care premisele, dacă ar fi adevărate, ar fi cea mai puternică dovadă posibilă că concluzia este adevărată. Într-adevăr, aceste argumente oferă următoarea garanție: dacă premisele sunt adevărate, atunci și concluzia trebuie să fie adevărată.
Un argument care pare a fi deductiv, dar care are premise care nu susțin concluzia (nicio garanție) este un argument invalid.
Să repetăm silogismul P => C (Premisele duc la concluzie).Există patru afirmații posibile pe care le puteți face în legătură cu acesta:

1. Toate premisele sunt adevărate (P este adevărat) (raționament modus ponens)
2. Una sau mai multe dintre premise este falsă (P este falsă – nu P)
3. Concluzia este adevărată (C este adevărată)
4. Concluzia este falsă (C este falsă – nu C) (raționament modus tollens)

Doar două dintre acestea (#1 și #4) constituie un raționament valid din punct de vedere deductiv.Să ne uităm la motivul pentru aceasta, câte o alegere pe rând.

1. P este adevărat (P) – Afirmarea antecedentului. Dacă toate premisele sunt adevărateconcluzia trebuie să fie adevărată. Acesta este un argument foarte puternic. (modus ponens)
2. P este fals (nu P) – Negarea antecedentului. Faptul că P este fals nu garantează că C este fie adevărat, fie fals. Pot exista și alte cauze.
3. C este adevărat (C) – Afirmarea consecventului. Dacă C este adevărat ar putea fipentru unul din mai multe motive, nu pentru acest P specific.
4. C este fals (nu C) – Negarea consecventului. Aici, dacă C este fals, atunciP trebuie să fie și el fals. Dacă P ar fi adevărat, C ar fi și el adevărat. (modus tollens)

În concluzie, #1 și #4 (modus ponens și modus tollens) sunt deductivvalide, în timp ce #2 și #3 nu sunt.
Dacă premisele se aplică la lucruri din lumea reală, tot trebuie să faceți un test de invaliditate. Există cel puțin trei abordări.

1. Vezi dacă poți găsi un scenariu în care premisele sunt adevărate, dar concluzia este falsă.
2. Încearcă să înlocuiești un substantiv sau adjectiv din argument cu un altul.Înlocuiește toate instanțele. Dacă în mod evident acest lucru nu este valabil, atunci originalul nu era valabil.
3. Reprezentați P și C într-o diagramă Venn.Dacă puteți face acest lucru astfel încât P să fie adevăratdar C să fie fals, argumentul este invalid. Am realizat aceste diagrame pentru voi mai jos.

Acum aducem în discuție subiectul diagramelor Venn. Acestea pot fi de mare valoareîn verificarea premiselor unui argument.

Diagramele Venn

Diagramele Venn sunt o metodă grafică de reprezentare a logicii.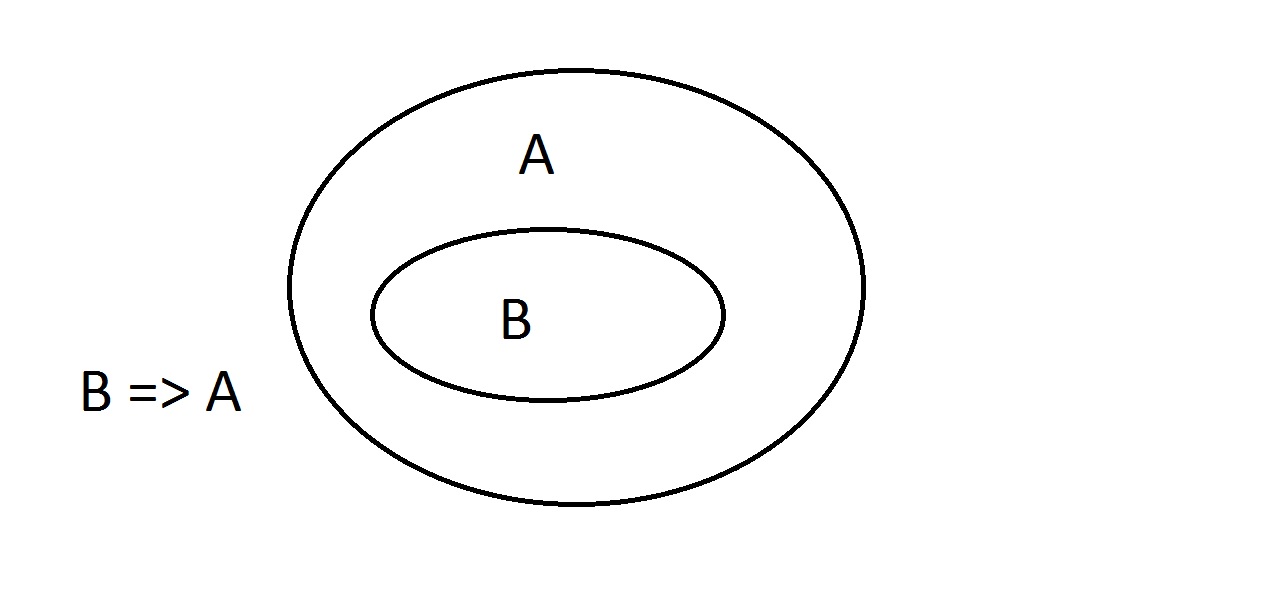
Aceasta este aproximativ cea mai simplă diagramă pe care o veți obține. Ovalul exterior conține toate lucrurile care auproprietatea A, în timp ce ovalul interior conține toate lucrurile care au proprietatea B, precum și proprietatea A.Aceasta este reprezentată sub forma B=>A, ceea ce înseamnă că toate lucrurile care au proprietatea B au și proprietatea A.Se poate spune, de asemenea, „B implică A. „Dacă B este adevărat, atunci și A trebuie să fie. Aceasta este garanția menționată mai sus.
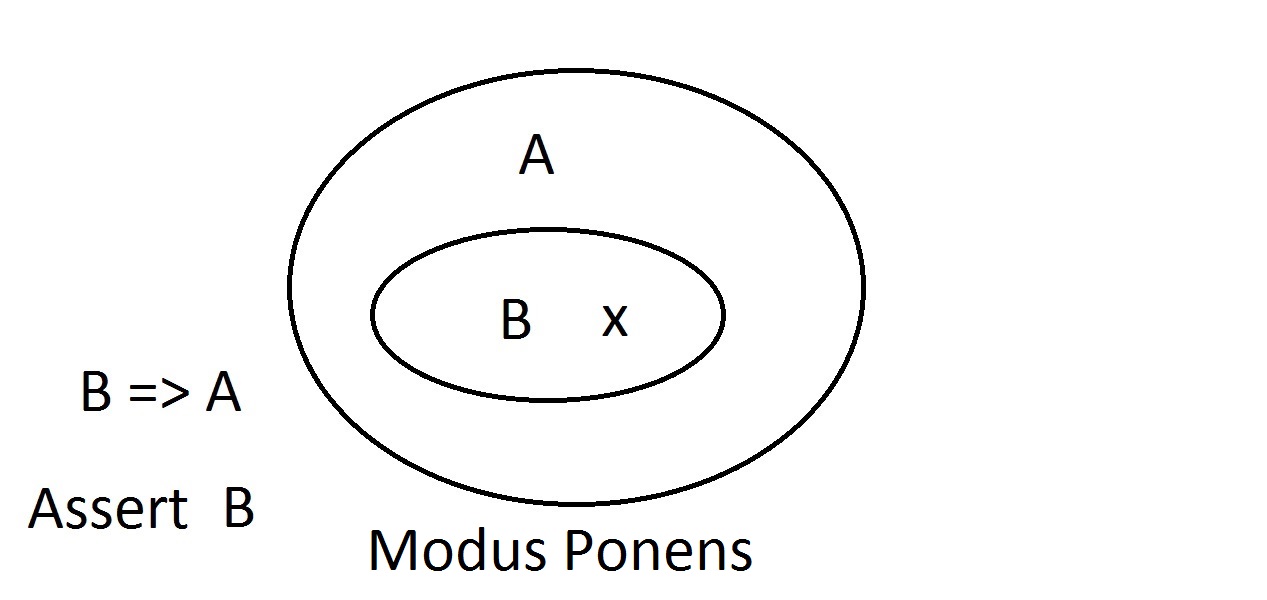Acum vom afirma că avem ceva cu proprietatea B. Putem afirma cu încredere că acesta are și proprietatea A. Acesta este un raționament Modus Ponens (afirmarea antecedentului). Orice entitatecu proprietatea B trebuie, evident, să se afle și în spațiul proprietăților A.
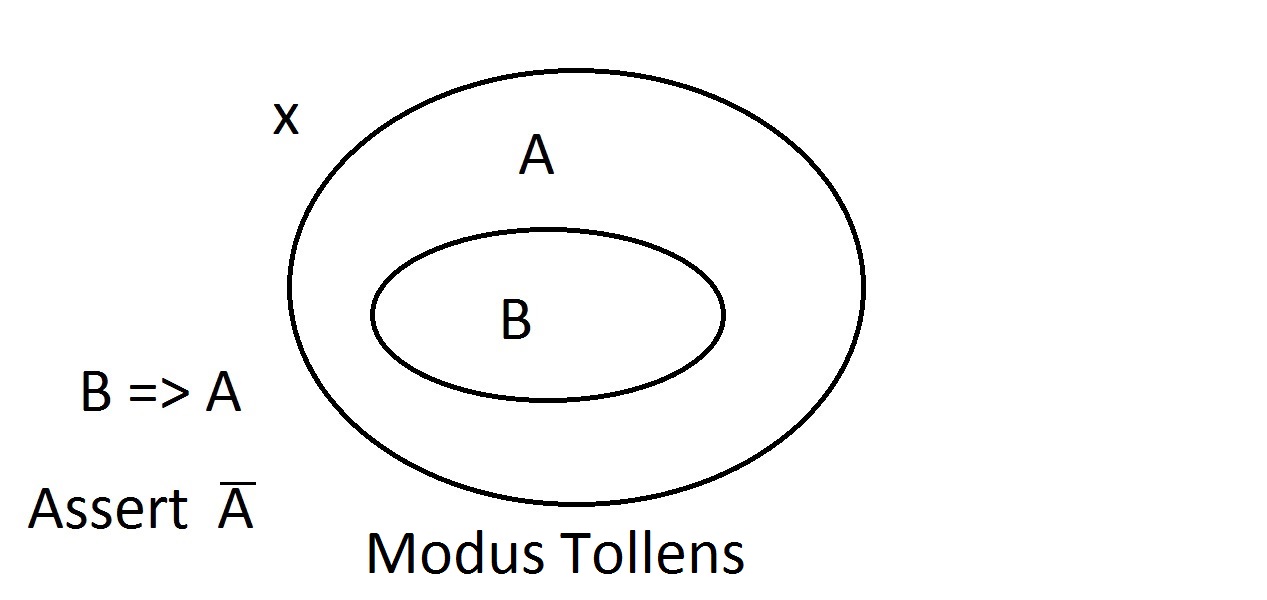Să presupunem că acum afirmăm că o entitate nu are proprietatea A. Diagrama Venn ne arată că nu poate avea nici proprietatea B. Orice lucru din afara spațiului proprietății Atrebuie să fie, de asemenea, în afara spațiului proprietății B. Acesta este un raționament Modus Tollens (negarea consecventului)și este valid și puternic.
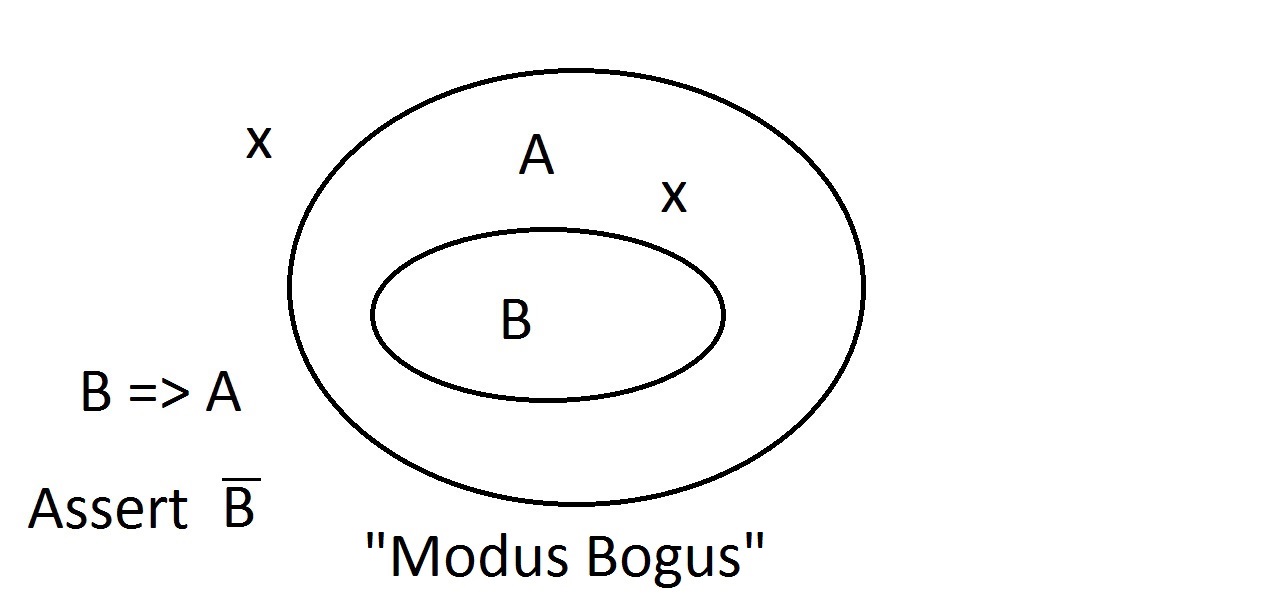Acum vom încerca să afirmăm că lucrul nostru nu posedă proprietatea B. O privire la diagramaVenn arată problema de aici. O entitate care nu are proprietatea B se poate afla în interiorul spațiului Asau în afara acestuia. Afirmația „nu are B” nu ne spune nimic despre A. Acesta nu este un raționament valid, așa că l-am numit Modus Bogus. Este negarea antecedentelor și nu este validă.
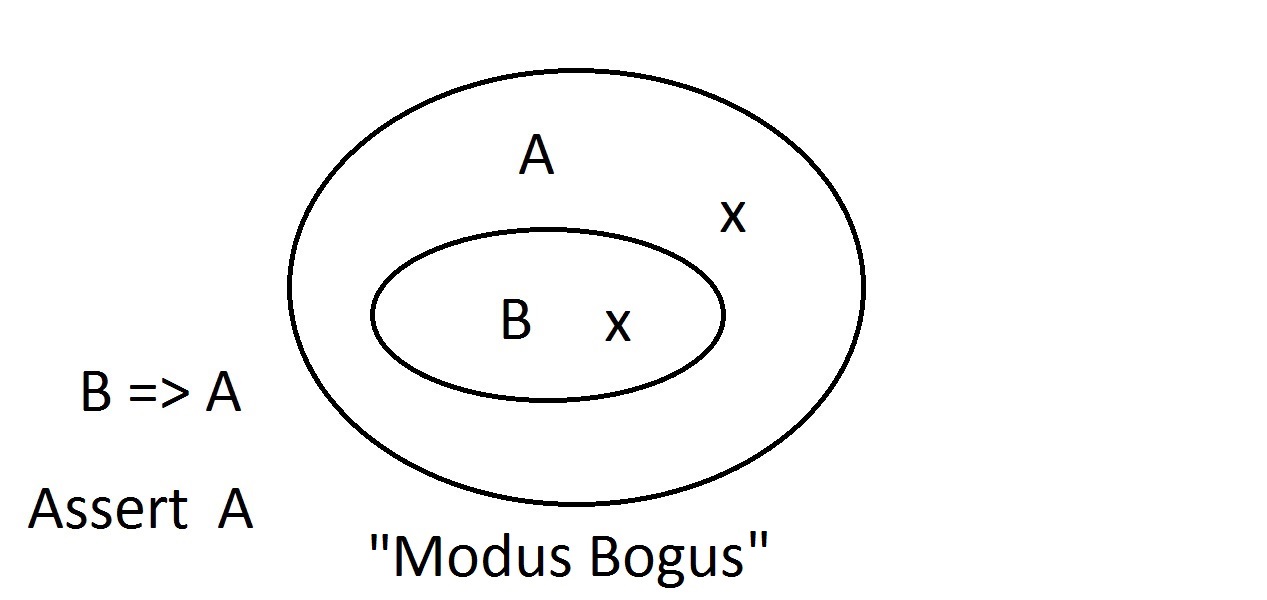Ultima posibilitate este să afirmăm că lucrul nostru are proprietatea A.Diagrama Venn arată problema. Entitatea s-ar putea afla oriunde în spațiul A,fie în interiorul sau în afara spațiului B. Afirmarea faptului că lucrul are proprietatea A nu vă spune nimic despre faptul dacă are și B. Acesta este, de asemenea, Modus Bogus, sau raționament invalid.Se numește Afirmarea consecventului.
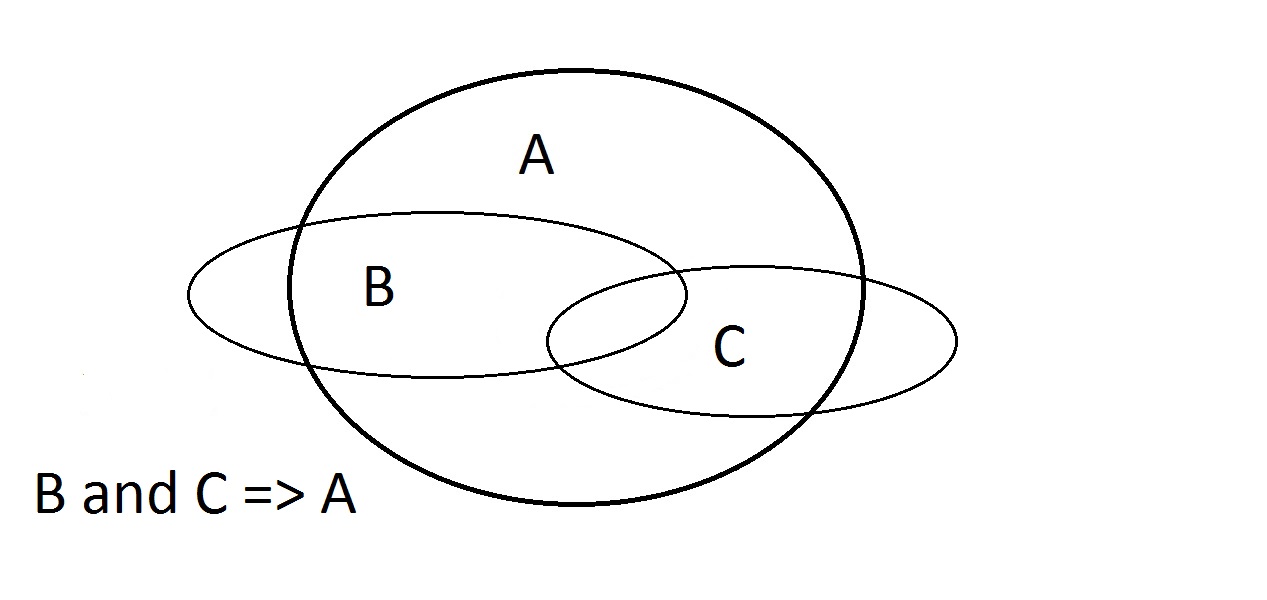Aici avem de-a face cu proprietățile A, B și C.Aici putem garanta doar că o entitate care are B și C are și A.Observați că unele dintre spațiile B și C se află în afara lui A.

• Afirmă A: Ar putea fi oriunde în A
• Afirmă B: O parte din B se află în afara lui A
• Afirmă C: O parte din C se află în afara lui A
• Afirmă A și B: Ar putea include o parte din C; ar putea să nu.
• Assert B și C: Intersecția BC se află în întregime în A. Argumentul că B și C => A funcționează.
• Assert A și C: Ar putea include o parte din B; s-ar putea să nu

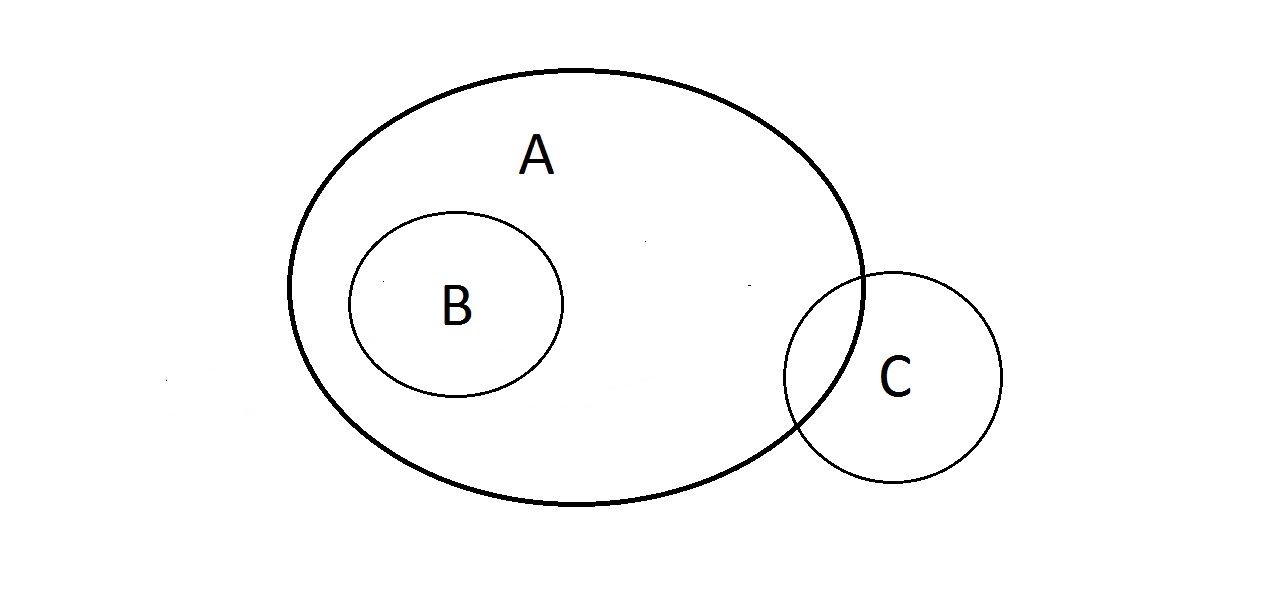
Ce poți face cu asta? Proprietățile A și B sunt ca mai sus, dar cum rămâne cu C? Ceva care are proprietatea C ar putea fi inclus în A sau ar putea să nu fie inclus. Ceva din A ar putea fi, de asemenea, în C sau nu. Nu puteți face nimic cu C aici. Avem însă garanția că ceva care îl are pe B îl are și pe A.

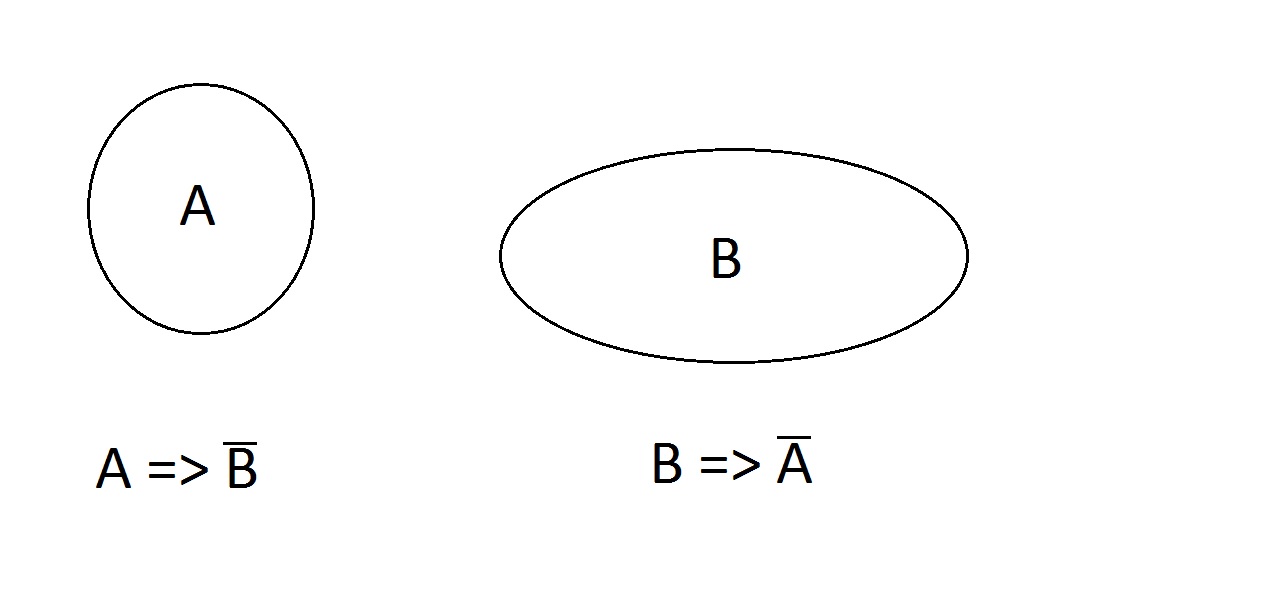
Ce ziceți de asta. Proprietățile sunt exclusive; o entitate nu le poate avea pe amândouă în același timp. poate să nu aibă niciuna, A sau B, dar nu și AB. Afirmațiile A=> nu B și B => nu A sunt valide.
În cele din urmă, dorim ca argumentul nostru să fie solid. Pentru ca acest lucru să se întâmple, argumentul trebuie să fie valid din punct de vedere deductiv ca mai sus și premisele trebuie să fie adevărate în lumea reală. Acest lucruînseamnă că toate argumentele solide sunt valide, dar toate argumentele valide nu sunt neapărat solide.

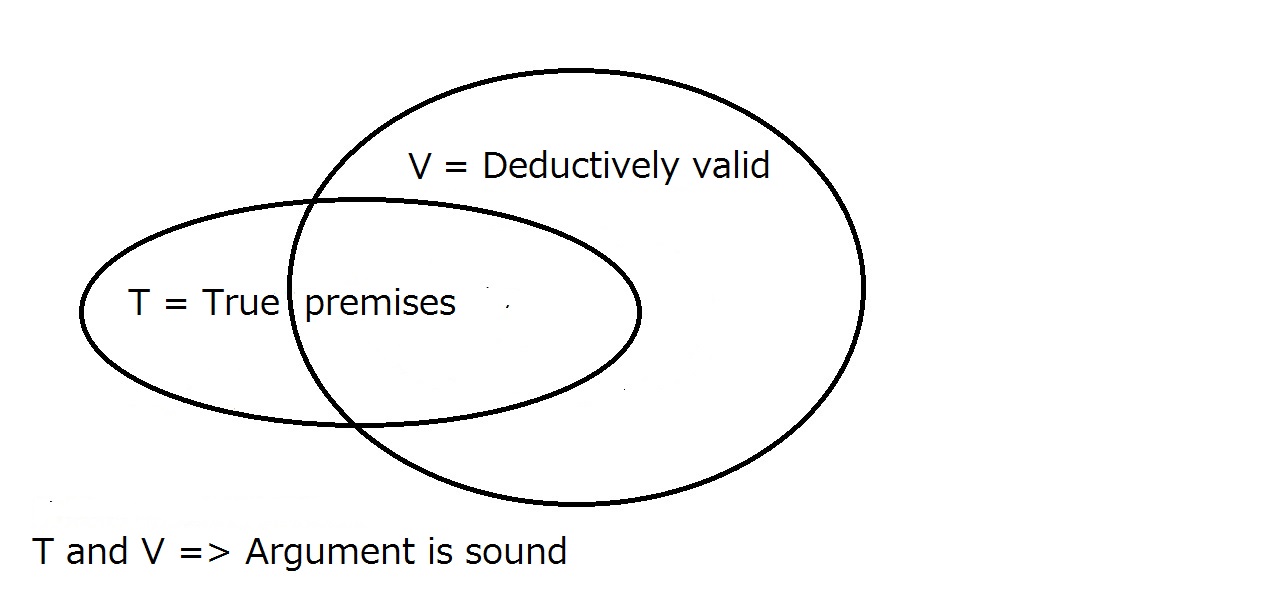
Un argument solid necesită să fie valid din punct de vedere deductiv și să aibă premise adevărate.Faptul de a avea una dintre ele nu o garantează automat pe cealaltă. Regiunea care se află în interiorul atât al luiT cât și al lui V este regiunea argumentelor solide.

Iată cum văd eu lucrurile. Toată lumea să mă asculte.

Aristotel (384-322 î.Hr.)

De la http://www.rwe.org/images/aristotle.jpgExperiment?
Autoconsistent?
Dacă teoria ta nu este autoconsistentă, sau dacă teoria ta nu este în dezacord cuexperimente minuțioase, atunci teoria ta este greșită. Nu contează cât de frumoasă este teoria; ea este greșită.

Galileo Galilei (1564-1642)

De la http://helios.gsfc.nasa.gov/galileo.jpg

de exemplu, al cincilea postulat al lui Euclid.

(1) Prin oricare două puncte diferite, este posibil să se traseze o singură linie.
(2) O dreaptă finită poate fi prelungită continuu în linie dreaptă.
(3) Un cerc poate fi descris având ca centru orice punct și ca rază orice distanță.
(4) Toate unghiurile drepte sunt egale.
(5) Printr-un punct dat, se poate trasa o singură linie paralelă cu o dreaptă dată.
Cuvintele „punct” și „linie” nu au nici o semnificație intrinsecă.
Se pot schimba „punct” și „linie” și tot se pot avea teoreme adevărate.
Se poate spune
(1) Prin două bariante diferite oarecare, este posibil să se traseze un fleem…
Cel de-al cincilea postulat poate fi schimbat în două moduri:
(5) Printr-un punct dat, nu se poate trasa nicio dreaptă paralelă cu o dreaptă dată.
(5) Printr-un punct dat, se pot trasa mai multe drepte paralele cu o dreaptă dată.
Ambele noi postulate dau naștere la geometrii CONSISTENTE diferite.Care dintre ele este corectă? Toate sunt corecte! Care dintre ele descrie acest Univers?Aceasta este FIZICA!
.