Související témata:
Další lekce algebry
Matematické pracovní listy
V této lekci se budeme zabývat syntetickým dělením, které je zjednodušenou formou dlouhého dělení.

Co je syntetické dělení?

Syntetické dělení je zkrácený způsob dělení mnohočlenu dvojčlenem ve tvaru (x + c) nebo (x – c). Dělení můžeme zjednodušit oddělením koeficientů.

Příklad:

Vyhodnoťte (x3 – 8x + 3) ÷ (x + 3) pomocí syntetického dělení

Řešení:

(x3- 8x + 3) se nazývá dividenda a (x + 3) se nazývá dělitel.

Krok 1:

Zapište konstantu dělitele se změněným znaménkem
-3

Krok 2:

Zapište koeficienty dividendy. (Nezapomeňte doplnit za chybějící členy koeficient 0)

Krok 3:

Zapište první koeficient.

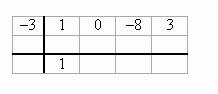
Krok 4:

Vynásobte (1)( -3) = -3 a přičtěte k dalšímu koeficientu.

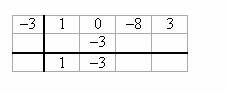
Krok 4 opakujeme pro všechny koeficienty

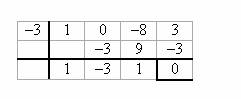
Zjistíme, že (x3- 8x + 3) ÷ (x + 3) = x2 – 3x + 1

Video

Syntetické dělení se snáze naučíme názorně. Podívejte se na následující videa, kde najdete další příklady syntetického dělení.

Polynomické dělení: Syntetické dělení
Provádějte syntetické dělení pro dělení binomu ve tvaru (x – k)
Příklad:
Dělení pomocí syntetického dělení
1. (2×3 + 6×2 + 29) ÷ (x + 3)
2. (2×3 + 6×2 – 17x + 15) ÷ (x + 5)
3. (y5 – 32) ÷ (y – 2)
4. (y5 – 32) ÷ (y – 2)
. (16×3 – 2 + 14x – 12×2) ÷ (2x + 1)

• Zobrazit řešení krok za krokem

Dělení trojčlenky dvojčlenkou pomocí syntetického dělení
Příklad:
Dělení pomocí syntetického dělení
1. (x2 – 5x + 7) ÷ (x – 2)
2. (x2 + 8x + 12) ÷ (x + 2)

• Ukázat řešení krok za krokem

Syntetické děleníToto video ukazuje, jak lze pomocí syntetického dělení dělit mnohočlen lineárním výrazem
Ukazuje také, jak lze syntetické dělení použít k vyhodnocení mnohočlenů.
Příklad:
(x3 – 2×2 + 3x – 4) ÷ (x – 2)

• Ukázat řešení krok za krokem

Syntetické dělení
Toto video ukazuje, jak použít syntetické dělení k dělení mnohočlenu lineárním výrazem a také jak použít zbytek k vyhodnocení mnohočlenu.
Příklad:
(x4 – x2 + 5) ÷ (x + 3)

• Ukázat řešení krok za krokem

Vyzkoušejte níže uvedenou bezplatnou kalkulačku a řešitele úloh Mathway k procvičení různých matematických témat. Vyzkoušejte si uvedené příklady nebo zadejte vlastní úlohu a zkontrolujte si odpověď pomocí vysvětlení krok za krokem.