Seuraavat aiheet:
Lisäoppitunteja algebraan
Matematiikan työpaperit
Tällä oppitunnilla tarkastelemme synteettistä jakolaskua, joka on pitkien jakolaskutoimitusten yksinkertaistettu muoto.
Mitä on synteettinen jako?
Synteettinen jako on lyhennetty tapa jakaa polynomi binomilla muodossa (x + c) tai (x – c). Voimme yksinkertaistaa jakoa irrottamalla kertoimet.
Esimerkki:
Valitaan (x3 – 8x + 3) ÷ (x + 3) käyttäen synteettistä jakoa
Ratkaisu:
(x3- 8x + 3) on nimeltään osingonantaja ja (x + 3) on nimeltään jakaja.
Vaihe 1:
Kirjoita jakajan vakio, jonka merkki on vaihdettu
-3
Vaihe 2:
Kirjoita jakajan kertoimet. (Muista lisätä kerroin 0 puuttuviin termeihin)

Vaihe 3:
Kirjoita ylös ensimmäinen kerroin.
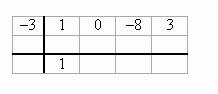
Vaihe 4:
Kerroin (1)( -3) = -3 ja lisää seuraavaan kertoimeen.
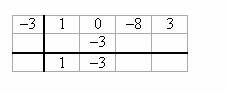
Toista vaihe 4 kaikille kertoimille
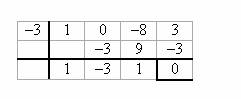
Havaitsemme, että (x3- 8x + 3) ÷ (x + 3) = x2 – 3x + 1
Videot
Synteettinen jakolaskenta opitaan helpommin visuaalisesti. Katso seuraavilta videoilta lisää esimerkkejä synteettisestä jaosta.
Polynomijako: Synteettinen jako
Toteuta synteettinen jako jakaaksesi binomilla muodossa (x – k)
Esimerkki:
Jaa käyttäen synteettistä jakoa
1. (2×3 + 6×2 + 29) ÷ (x + 3)
2. (2×3 + 6×2 – 17x + 15) ÷ (x + 5)
3. (y5 – 32) ÷ (y – 2)
4. (16×3 – 2 + 14x – 12×2) ÷ (2x + 1)
- Näytä vaiheittaiset ratkaisut
Jaa trinomi binomilla käyttäen synteettistä jakoa
Esimerkki:
Jaa käyttäen synteettistä jakoa
1. (x2 – 5x + 7) ÷ (x – 2)
2. (x2 + 8x + 12) ÷ (x + 2)
- Näytä vaiheittaiset ratkaisut
Synteettinen jakoTällä videolla näytetään, miten voit käyttää synteettistä jakoa jakamaan polynomin lineaarisella lausekkeella.
Se näyttää myös, miten synteettistä jakoa voidaan käyttää polynomien arviointiin.
Esimerkki:
(x3 – 2×2 + 3x – 4) ÷ (x – 2)
- Näytä vaiheittaiset ratkaisut
Synteettinen jako
Tällä videolla näytetään, miten synteettistä jakoa voidaan käyttää polynomin jakamiseen lineaarisella lausekkeella ja miten jäännöstä voidaan käyttää myös polynomin arviointiin.
Esimerkki:
(x4 – x2 + 5) ÷ (x + 3)
- Näytä vaiheittaiset ratkaisut
Kokeile alla olevaa ilmaista Mathwayn laskinta ja ongelmanratkaisijaa harjoitellaksesi erilaisia matematiikan aiheita. Kokeile annettuja esimerkkejä tai kirjoita oma ongelmasi ja tarkista vastauksesi vaiheittaisten selitysten avulla. 

